Анти-неустойчивость - «Эзотерика»

На почтовых посылках, бывает, пишут: «хрупкое», «бьющееся» или «обращаться осторожно!». Но представим себе полную противоположность: посылку с надписью «обращаться небрежно!» или «обращаться как угодно!». Содержимое посылки в таком случае не просто небьющееся и невосприимчивое к ударам — оно обладает чем-то большим, поскольку способно извлекать из ударов пользу. Предлагаю для всего того, что в среднем (т.е. в перспективе) выигрывает от непостоянства, новое обозначение «анти-неустойчивый». Чтобы понять, насколько чужда подобная идея нашему сознанию, спросите у знакомых антоним слова «неустойчивый». Ответы, вероятно, будут: устойчивый, стабильный, прочный, крепкий, сильный и т.д. Неправильно. И в данном случае заблуждаются не только отдельные индивиды, но и целые разделы знаний. Эту ошибку содержит любой словарь. Попросите того же самого человека назвать противоположность разрушению, он ответит: сооружение либо создание. Или спросите антоним слова «вогнутость» — вам ответят: выпуклость. Вербальное определение выпуклости: от изменений она скорее выигрывает, чем проигрывает; вогнутость — ее противоположность. В этом ключ, когда я пытался дать математическое определение неустойчивости (используя суммы зависящих от пути функций выигрышей), я обнаружил, что «неустойчивое» может быть описано в терминах вогнутости к источнику изменений (случайных или неслучайных). А противоположность этому, разумеется, — выпуклость. Пусть здоровье бабушки неустойчиво, а следовательно, соответствует вогнутой функции. Что бы вы предпочли — оставить ее на час при 0°С и еще на час при 50°С или на два часа при 25°С? В обоих случаях средняя температура одинакова, но в первом случае она крайне изменчива, а во втором — стабильна, и именно он предпочтительнее для бабушки. Более того, можно быть неустойчивым к одним событиям, а к другим — нет. Портфель ценных бумаг может быть слегка вогнутым в отношении небольшого падения на рынке, но не в случае крайне больших отклонений — «черных лебедей» (событий, которые кажутся неожиданными, имеют далеко идущие последствия, а в ретро­спективе — закономерные объяснения). 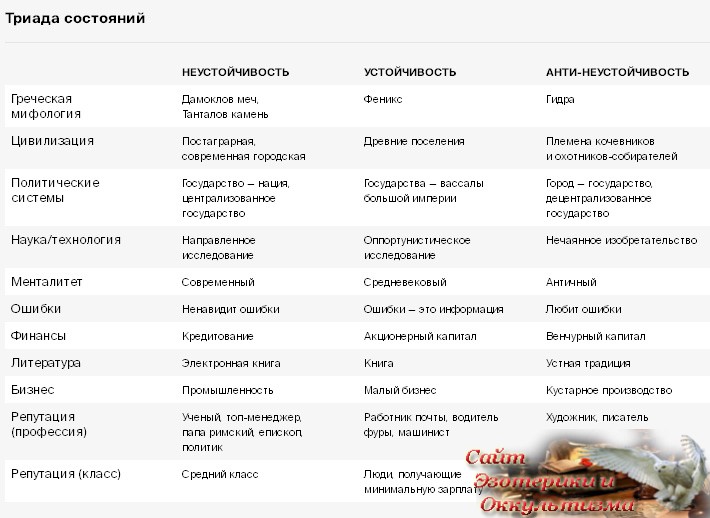Эволюция (отчасти) является выпуклой функцией в ситуации изменений, до некоторых пределов неустойчивость и множественные факторы стресса идут живым организмам на пользу, поскольку ДНК выигрывает от разнообразия среди потомства. Метод проб и ошибок — выпуклая функция, потому что стоимость ошибок невелика, а выгода может быть большая. Проявления выпуклых и вогнутых функций в различных аспектах нашей жизни суммированы в таблице «Триада состояний». Чем больше корпорация, тем более она вогнута по отношению к определенному давлению (хотя крупные компании и заявляют о том, что выигрывают на экономии масштаба, статистика свидетельствует, что чем они больше, тем менее они устойчивы к событиям из разряда «черных лебедей», причем неустойчивость эта крайне диспропорциональна). То же самое происходит с государственными проектами: большое правительство способствует неустойчивости. Как правило, большинство иерархически организованных систем становятся неустойчивыми. Экономические теории создают модели, которые часто способствуют неустойчивости, что объясняет, почему использование этих моделей гораздо хуже, чем ничегонеделание. Так, финансовые модели, основанные на «управлении рисками» редких событий, — это шутка. Чем меньше вероятность, тем более выпуклой она становится к ошибке в вычислениях (а выигрыш тем более выгнутым): 25-процентная ошибка в оценке стандартного отклонения гауссовой кривой может увеличить ожидаемые потери в результате удаленных событий в миллиард раз! (Невнимание к этому простому замечанию продолжает разрушать банковскую систему.) А теперь главное. Посредством простого математического свойства (выпуклости и вогнутости) можно показать, почему в условиях модели неопределенности пункты, перечисленные в правой колонке таблицы, в долгосрочной перспективе выиграют и преуспеют в большей степени, чем может показаться на первый взгляд, тогда как перечисленные в левой колонке — обречены на вымирание. За последнее десятилетие менеджеры компаний заработали в совокупности триллионы, тогда как пенсионеры триллионы потеряли (топ-менеджеры берут позитивные, а не негативные риски, и это дает им «свободный выбор» выпуклой функции выигрыша). Так же напористое изобретательство окупается куда лучше, чем направленное исследование. Почему? Неравенство Йенсена говорит следующее: для выпуклой функции выигрыша ожидание среднего будет выше, чем среднее ожиданий. Для вогнутой — наоборот (здоровье бабушки будет хуже, если температура будет в среднем 25°С, чем если средняя температура будет 25°С). Возведение в квадрат — выпуклая функция. Возьмите обычную игральную кость, и пусть выигрыш равен номеру, на который падает кость. Средний выигрыш — 3,5, его квадрат равен 12,25. Теперь предположим, что мы взяли квадрат номеров на сторонах игральной кости — 15,1666. Таким образом, среднее квадрата выигрыша выше, чем квадрат среднего выигрыша. Последствия могут быть удивительными, поскольку этот побочный эффект объясняет множество тайн истории. В перспективе же все, что любит «черных лебедей», останется в будущем. Все, что их боится, в конечном счете исчезнет в пределах своей вогнутости. Автор: Нассим Николас Талеб, математик, философ, специалист по анализу рисков, профессор Нью-йоркского университета. Esquire